Recently, Hanno Ix, a retired engineer and a member of the online NavList navigation forum (www.fer3.com/arc/), presented a challenge to the forum for the development of a manageable means of sight reduction without the use of logs, slide rules or calculators and, if possible, also eliminating special rules and ambiguities.
The group took up the challenge and we began with the classic Law of Cosines navigational triangle formula:
Sin h = Sin L Sin d + Cos L Cos d Cos t
This formula requires three time-consuming, error-prone multiplication steps. The next effort centered on the Davis haversine/cosine formula:
hv ZD = hv (L ~ d) + hv (t) Cos L Cos d
(L~d is the same as L +/- d — L – d when latitude and declination are the same name and L+ d when contrary name.)
This formula was almost manageable with two multiplication steps but is still classified as time consuming and error prone.
The breakthrough came with the discovery of the haversine/cosine Doniol formula in the 1977 Volume No. 1 of Bowditch. The beauty of this formula caught my eye as I was leafing through the pages. Very close to perfect, with just a single multiplication step and a few special case rules:
Sin h = n – (n+m)a
n = Cos (L – d) m = Cos (L + d) – same name
n = Cos (L + d) m = Cos (L – d) – contrary name
a = hv (t)
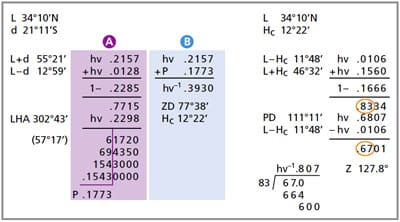
The haversine/cosine Doniol formula was rewritten by forum member Hanno Ix to all haversines that have only one multiplication step and no special rules. Beauty was looking me square in the eye:
 |
|
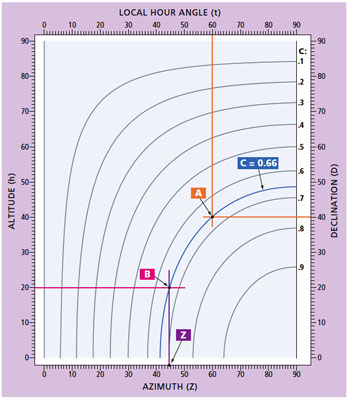
Hanno Ix’s azimuth graph. Step 1: Mark dec. on right scale, draw horiz. line. Step 2: Mark LHA on top scale, draw vert. line, it intersects horiz. line at “A.” Step 3: Mark alt. on left scale, draw horiz. line, it intersects curve “C” at “B.” Step 4: draw vert. line through pt. “B” and line intersects bottom axis to indicate azimuth: 44. |
|
Pat Rossi/Navigator Publishing |
hv ZD = n + [ 1 – ( n + m) ] ( a )
n = hv (L – d) m = hv (L + d) same name
n = hv (L + d) m = hv (L – d) contrary name
a = hv (t)
ZD = Zenith Distance
Hc = 90 – ZD
L = Latitude
d = Declination
t = Meridian Angle
hv = Haversine
Azimuth is solved with Hanno Ix’s fantastic azimuth graph. I developed an “index card” version of the process see diagram.
Here’s a summary of benefits for the all haversine Doniol sight reduction longhand method:
1. Full coverage of latitudes and declinations
2. Uses DR as the assumed position
3. No special rules
4. Ultra compact
5. Quick solution time
6. 1’ precision
7. Not reliant on electronics or mechanical devices.
Greg Rudzinski is a retired merchant mariner who lives aboard a Bruce Roberts Offshore 38 ketch at Channel Islands Harbor, Oxnard, Calif.