Editor’s note: We’re revisiting this series on navigating by the sun, moon, planets and stars in the age of GPS because celestial nav is not only a viable backup to satellite navigation, but it is also a skill that ocean voyagers should have in their toolkit. In this series, we’ll cover all the basic knowledge you’ll require to get up to speed on this elegant and rewarding technique for finding your way at sea. Click to read Part 1, Part 2, Part 3, Part 4, Part 5, Part 6, Part 7, Part 8, Part 9 and Part 10.
In this installment, we’ll cover how to reduce a noon sight and also how to get latitude by shooting Polaris, the pole star.
Possibly the easiest and quickest way of getting a line of position (LOP) from a sun sight is at noon. A noon sight can be reduced for latitude quickly and easily without any need to use sight reduction tables.
To take a noon sight, first precalculate the time of local apparent noon (LAN). The noon sight is not taken at 1200, but rather when the sun is on the observer’s meridian of longitude-meridian passage. Although this is based on the meridian passage at 0°, which is listed in the daily pages, the time at any given longitude may differ.
 |
|
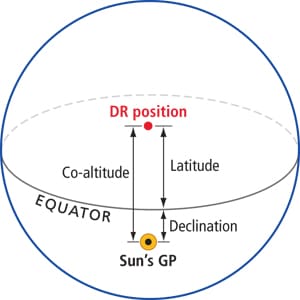
Both your latitude and the sun’s declination are north, but the sun is north of you. Latitude = declination – co-altitude. |
To precalculate the time of LAN, start with the time of meridian passage from the bottom of the right-hand daily page. To find out how long it will take for meridian passage to get to your longitude, take your DR longitude back to the arc-to-time conversion table on the first colored page in the back of the Nautical Almanac. If the longitude is west, this should be added to the time of meridian passage. Subtract it from meridian passage if the longitude is east.
Head up on deck five or 10 minutes beforehand and bring the sun down to the horizon with the sextant. During the next few minutes, the sun will continue to rise. Then it will hang, neither rising nor setting. This is the time to record your sights. After a minute or two, the sun will begin to descend.
Correct from Hs to Ho just like any other sun sight.
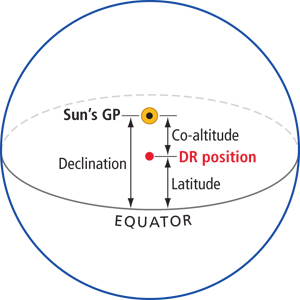
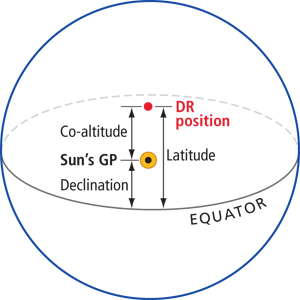
With this noon sight, we are just trying to determine the distance from the equator to our position (in the case of the noon site to our latitude). When the sun crosses our meridian of longitude, it is either due south or due north of us; the resulting LOP runs east/west, just like a line of latitude. So for all intents and purposes, our LOP is our latitude. To determine latitude, use the relationship between the sun’s declination, co-altitude (90° – Ho) and latitude. In the accompanying diagrams, we illustrate the various relationships between these elements.
 |
|
Both your latitude and the sun’s declination are north, but the sun is south of you. Latitude = declination + co-altitude. |
Because we have Ho, the co-altitude is easy to determine. Declination needs to be looked up in the Nautical Almanac daily pages, just as for any sight. Don’t waste any time on GHA; you don’t need it.
Lastly, find the correct formula to plug co-altitude and declination into. The easiest way to determine this is to just sketch out a small diagram showing the relative position of the observer, the sun and the equator. It doesn’t have to be exact; its purpose is only to show the relationships between the elements so you know what to subtract from what to get latitude.
Sample problem
On Sept. 7, your DR position is 34° 12’ N and 64° 02’ W. What will be the time of meridian passage?
The time of meridian passage at 0° on Sept. 7 is 1158. Taking 64° W to the arc-to-time conversion table gives a correction of 0416.
| meridian pass. at 0° corr. for 64° W meridian pass. at 64° W |
1158 GMT + 0416 1614 GMT |
If the Ho (Hs corrected for index error, dip and the main sun correction) is 61° 45.1’, find the latitude.
Since we know Ho, next find the declination. It is 5° 59.2’ N at 1600. The d is –0.9, and looking up the correction at 14 minutes we get –0.2’.
| declination d correction declination |
N 5° 59.2’ – 0.2’ N 5° 59.0’ |
Next, determine the co-altitude based on Ho.
|
Ho co-altitude |
90° – 61° 45.1’ 28° 14.9’ |
Now, all that is left is to combine co-altitude and declination. The formula we want is the one where both our position and the sun’s position are in the Northern Hemisphere and we are to the north of the sun. That is latitude = co-altitude + declination.
| co-altitude declination latitude |
28° 14.9’ + 5° 59.0’ N 34° 13.9’ |
Plot this by drawing an LOP through 34° 08.4’ N parallel to other lines of latitude and labeling it.
Longitude from the noon sight
Sights taken at noon can also provide you with longitude, making it possible to get a fix from the sun at LAN. This does not require the use of any tables except for the Nautical Almanac. The difficulty is finding the exact time of LAN. That is impossible with a sextant alone because the sun appears to hang at the same altitude for a few minutes and the true time of meridian passage can’t be determined solely via observation.
There are two methods for determining the time of LAN. The first will appeal to those more comfortable with numbers; the latter for those happier with graphs.
Start taking sights about 20 to 25 minutes before LAN. At first, take them at five- or 10-minute intervals as the sun rises. When the sun hangs, shoot it for latitude.
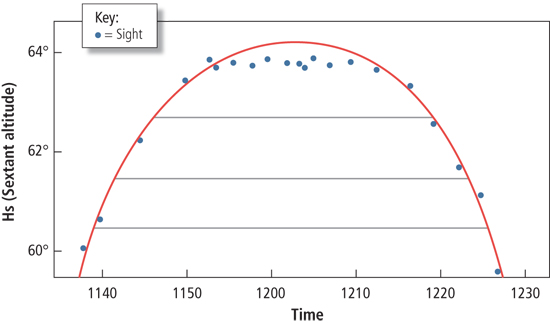
Once the sun begins to descend, set the sextant to the last Hs that you recorded before LAN. Note the time that the sun is at that altitude and then preset for the next lower Hs. Three of these corresponding Hs readings should suffice.
Take two sights with the same Hs and find the difference in the times of the sights. Divide that by two and add it to the time of the earlier sight. Do this for two or three sets of sights, then average the results and use that as the time of LAN.
 |
|
The horizontal lines connect two times when the sun was at the same altitude. Theoretically, the meridian passage should be exactly between these times. To find that, the two times on each end of the horizontal lines must be ascertained and then averaged. This averaged time is the time of meridian passage. |
The second method begins similarly: Take sights every five or 10 minutes in the 25 minutes before LAN. As the sun descends, just shoot every five or 10 minutes unconstrained by the Hs (this is sometimes called the laid-back approach).
Now graph the results: Hs on one axis, and time on the other as shown here. Freehand in a curve that averages these points. Now, draw a line from any Hs and determine the two times the sun was at this Hs on the graphed curve. From here it is just like the last method.
The final averaged time is, theoretically, the exact time of LAN. Find the GHA of the sun at that time. That GHA is your longitude in the Western Hemisphere. In the Eastern Hemisphere, longitude = 360° – GHA.
One peril with finding longitude at noon is that the boat moves. Even at 6 knots, a sailboat will move four miles in 40 minutes. This may affect the longitude that you determine. The effect will be greatest heading north or south. There will be no effect for a vessel headed east or west.
 |
|
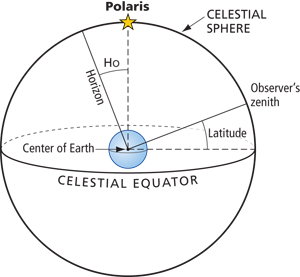
The relationship between the Ho of Polaris and the observer’s latitude. The 90° angle formed by the north celestial pole (and therefore Polaris) through the observer on Earth to the celestial equator, and the 90° angle formed from the zenith to the observer to the horizon make this possible. The arc from Polaris to the observer’s zenith is common to both 90° angles. Thus the distance from the horizon to Polaris must be the same as the distance from the equator to the observer’s zenith (essentially the observer’s latitude). |
Latitude from Polaris
Polaris, the North Star, is almost, but not quite, over the North Pole. Because it is so close to the pole, it does not set during the night. Polaris may be used as a quick way to determine true north and it also provides an easy way to determine latitude.
Since it isn’t one of the brighter stars, Polaris can be difficult to shoot, so at dawn try to shoot it as soon as the horizon is visible because it will be one of the first navigational stars to disappear. At dusk, you can preset your sextant to the DR latitude and search.
Roughly speaking, the angle of the pole over the horizon equals latitude. With a few quick corrections, one sight of Polaris can be reduced to latitude.
First, correct Hs to Ho just the same way that it would be corrected for any star sight. Next, find the LHA Aries at the time of the sight. This is used to determine where Polaris is in its orbit around the pole. Now enter the Polaris tables starting on page 274 of the Nautical Almanac. The formula for determining latitude is found right at the bottom of the page:
Latitude = Ho – 1° + A0 + A1 + A2
To use the table, find the column for the LHA Aries and move down the column to the correct row for your LHA Aries. Write down the value found there. Continue down the same column to the section for A1. Find the correct row for your DR latitude and note that value. Continue down, staying in the same column. Find the value for the proper month.
Now subtract 1° from Ho, and then add the three corrections to get latitude.
Sample problem
On Oct. 12, you shoot Polaris and correct the Hs to an Ho of 39° 32.2’. The LHA Aries is 136° and the DR latitude is 39° 46’.
Enter the Polaris tables in the column for 130°-139° and move down to the row for 6°. The correction here is 1° 07.1’ (the 1° is not printed for each row). Moving down to the section for latitude, take the value for 40°, which is 0.5’. Finally, down to the section for the month of the year. The correction for October is 0.3’.
Begin by subtracting 1° from Ho and then add the corrections.
| Ho
A0 |
39° 32.2’ – 1° 00.0’ 38° 32.2’ + 1° 06.8’ + 0.5’ + 0.3’ 39° 39.8’ |