Nearly a century ago, powerboat design, to paraphrase Yogi Berra, “came to a fork in the road and took it.” We may have chosen the “wrong fork.” In light of today’s ever-rising fuel costs, this appears to be no idle concern. If a few things had gone otherwise early on, we might well be tooling around in voyaging powerboats that looked quite different from what we currently think of as “normal” boats.
Think of offshore powerboat racing and you probably picture 50- to 60-foot, macho, deep-vee muscle boats — and fuel consumption on the order of 180 gallons an hour!
Most sailors (power or sail) have at least heard of the Bermuda Race. Dreamed up by Thomas Fleming Day, the founding editor of Rudder magazine, the Bermuda Race — with a few minor gaps due to wars — has been held almost every other year since 1906. Now, Day’s intent was to improve both sailing yacht design and construction, and sailors’ confidence in going offshore.
 |
|
The 40-foot power racer Dream in heavy weather on the way to Bermuda. Despite having only a 16-hp engine, Dream won the New York to Bermuda race in 1912. |
The forgotten race
Sadly, it’s largely forgotten that the very next year (1907) the irrepressible Day, sponsored a powerboat race from New York to Bermuda. Not only did he initiate the race, but he skippered one of the entrants. Again, Day’s intent was to prove that small internal-combustion-engine craft were safe and reliable offshore. This was — at the time — a downright crackbrained point of view. Steam was the only power plant suitable for ocean work . . . everyone knew that!
The 1907 Bermuda Powerboat Race had two entries, Ailsa Craig and Idaho. Both were long, slender 60-footers. Ailsa Craig was powered by a single 65-hp gas engine, and Idaho by a 25-hp machine. You’d think that Idaho wouldn’t have stood much of chance — with that power difference — but there was a handicap formula that gave Idaho a reasonable shot to win on corrected time. Nevertheless — in this case — Craig (skippered by none other than Day himself) did win. Winning time was two days, 16 hours, and 20 minutes — a nice, leisurely ocean passage. If two boats taking between two and three days to run 650 miles doesn’t seem impressive, remember the year. Day later wrote in Rudder:
“Until the finish of the race, the name ‘internal combustion engine’ was a joke, only good enough to understudy steam. The race has demonstrated to the whole world that the internal combustion engine is reliable, and if it is reliable, it is adaptable to all commercial purposes!”
This first offshore powerboat race was critical in convincing people to buy new powerboats of all types.
This wasn’t the last Bermuda Powerboat Race. One was held every year up to 1914, except for 1911. There was even a return race back from Bermuda in 1909 and in 1912. World War I, however, finished the competition for good.
A good influence lost
It wasn’t only the bigger fellows who won this race, by the way. In 1912, Dream — a 40-footer with just a nine-foot beam and a single 16-hp engine (yep, only 16 horses) — beat its 50-foot competitor, the 25-hp Kathemma. These power ratings give one indication of the reason it’s such a pity that the Bermuda Powerboat Race has been forgotten. Ailsa Craig, with 65-hp (the most power entered in the race’s history), consumed about four and a half gallons per hour, burning up a total of 290 gallons on the entire trip! Compare this to airplane fare for your entire family. If only the Bermuda Powerboat Race had continued after World War I, modern voyaging powerboats would likely be rather different — somewhat slower, longer and more slender, and very fuel efficient. Superb seaboats as well.
A modern cruising Ailsa Craig, around 13,700 pounds, would be fitted with, say, a single 300-hp diesel or twin 150s. Cruise would be around 13 knots making the trek from New York to Bermuda in just over two days. This would cost you no more than 520 gallons of fuel for the hop over, and you could take your whole family, a friend or two, and all your belongings. Spend seven or eight days exploring the islands, then turn around and head home. This would be one pleasant and economical vacation. Slow down to 11 knots and the crossing would take you all of two and a half days and you’d use only 370 gallons of diesel.
How to make an efficient boat
I’ve read a lot about efficiency on boats over the years and much of it hasn’t added up. Almost any knowledgeable designer will tell you that just three basic things make for efficiency:
1) Going slower
2) Long, slender hulls
3) An efficient propulsion package
I’d like to make this seem more complicated, but that’s it. Yes, you can improve efficiency with tweaks and adjustments to the hull form. Also, certainly, the hull form must be properly matched to the intended operational speed, but hull-shape refinements add small percentages to efficiency, the three items above are — by a good margin — the overriding factors.
Transport efficiency
The bottom line is fuel consumption and this is what determines how efficient a powerboat is. How much fuel it takes to get it from point A to point B. Naval architects have a specific formula for efficiency, which is called “transport efficiency,” or “ET.” There are minor variations of ET. Ship designers are really interested in the weight of cargo moved from place to place efficiently. Transport efficiency for cargo ships is thus:
ET = speed x cargo weight ÷ power
Since fuel consumption is directly proportional to power, dividing by power gives you the efficiency.
In yachts, patrol boats, and small passenger vessels, it’s really the entire weight of the fully-loaded boat that should be evaluated, so for our purposes transport efficiency would be:
ET = speed x loaded displacement ÷ power
Engineers are fussy about units (for good reason), and to be more accurate we should define ET as:  (The 5.144 converts knots to meters per second and keeps all the units consistent.)
(The 5.144 converts knots to meters per second and keeps all the units consistent.)
Or in English units: 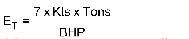 (The units here aren’t internally consistent but, instead, are set up to give the same result as the standard metric ET.)
(The units here aren’t internally consistent but, instead, are set up to give the same result as the standard metric ET.)
Where:
ET = Transport efficiency
Kts = Boat speed, in knots
Tonnes = Metric tons
Tons = Long tons of 2,240 pounds
kW = Total installed propulsion power, kW
BHP = Total installed engine power, brake horsepower
Propulsion efficiency
Almost all ordinary boats are driven by propellers. (Jets are the other alternative.) Except for high-speed boats, the larger the propeller diameter and the slower the shaft rpm, the more efficient the propulsion. Remember, for large diameter you need low shaft rpms. Indeed, one of the most frustrating things I run up against as a designer is finding deep reduction gears to mate with smaller engines — engines less than 300 or 400 hp. It’s like looking for a unicorn. No one seems to make them.
Comparing boats
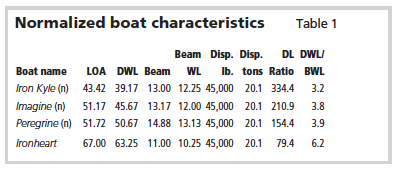
In order to clearly see the effects of our three basic efficiency criteria: going slower, slender hulls, and efficient propulsion, we can compare four different boats. In fact, there are four designs form my office: the long and very slender 67-foot Ironheart, the medium-slender 57-foot Imagine, the 47-foot ultra-shoal (27-inch draft), medium-slender, beachable tunnel-drive Peregrine/Nancy Lakin, and the rather solid chunk of a tug yacht, Iron Kyle at 45 feet.
Though we could make the comparison using the non-dimensional transport efficiency alone, it makes it easier to follow if all the boats are the same size. The important consideration here is that size is not length but displacement (weight), which is the same as volume. Accordingly, I’ve normalized the Imagine, Peregrine, and Iron Kyle designs to the same 45,000-pound displacement as Ironheart. I’ll refer to the normalized example boats using the designation (n). Thus, our four comparison boats are shown in Table 1.
 |
 |
 |
 |
Obvious differences and “normal” boats
The differences between these normalized boats are obvious and they are primarily in how long and slender (or wide and beamy) they are. The DL ratio (displacement-length ratio) is the clearest indicator and the lower the DL ratio the longer a boat is for its weight. You could, however, get a low DL ratio with a wide hull that was very flat and shallow. The other indicator is simply DWL divided by BWL (datum waterline length divided by beam waterline), also called “length-to-beam ratio.”
Interestingly, the seemingly rather chunky tug yacht Iron Kyle has a DL ratio of 334 and a DWL/BWL ratio of 3.2:1. Though heavy and beamy compared to the other boats in our sample group, both a DL of 334 and a length-to-beam ratio of 3.2:1 are not at all unusual these days. Many so-called trawler yachts are in this range. Indeed, there’s nothing specifically “wrong” with a heavy, beamy boat, but — what we’re discussing here is efficiency. It’s the fact that boats of such proportions are not uncommon which indicates that we may have taken that “wrong fork” in design so long ago.
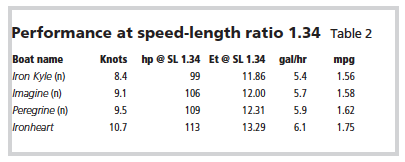
The common, and as we’ll see in a bit, not correct belief is that so-called displacement hulls are limited to a fixed hull speed. This is a speed-length ratio (SL ratio) of 1.34. The results in Table 2 assume we drive all three boats to an SL ratio of 1.34.
You can see that at nearly the same power, the longer, slender boats go faster. More important, the transport efficiency is higher for the longer and more slender the boat is. This is reflected in higher nautical miles per gallon — in improved mileage.
Slender hulls mean higher “hull speeds”
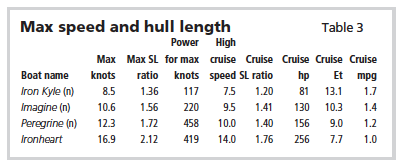
It gets better still for slender hulls. The fact is that the rule-of-thumb “hull speed” is not accurate. Maximum hull speed is not a constant 1.34 times the square root of the waterline in feet. Instead, the constant 1.34 is a variable and that variable is proportional to DL ratio. The formula I’ve developed that defines this relationship is:
Max hull SL ratio = 8.26 ÷ (DL ratio)0.311
But never less than 1.34.
This gives the maximum speed-length ratio a hull can be driven without planing. Applying this to our example boats, we get the results in Table 3.
This data shows just how much faster long, slender hulls can be driven without planing. Of course, going faster uses more power on any hull form (long and slender or short and wide) and this shows up as lower transport efficiencies and miles per gallon at the higher speeds. The important thing here is that the longer boats can be driven at these speeds, where the short wide boats can’t — at least without modifying their hulls.
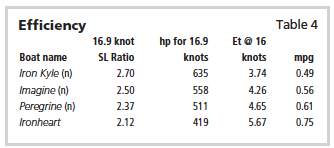
Indeed, the wider, shorter boats Iron Kyle (n) and Imagine (n) can’t be driven anywhere close to the 16.9 knots of the very slender Ironheart, though you’ll note that the medium slender Imagine (n) can achieve a max SL ratio of 1.56. You can take hulls of these displacements, and overall hull proportions and modify them — by giving them planing-hull characteristics — to allow them achieve 16.9 knots. They would then be true semi-planing hulls. The resulting power required is shown in Table 4.
Once again — if we drive to the same high speed the slenderest hull is capable off — we see just how much more efficient more slender hull forms are. The transport efficiency and miles per gallon delineate this clearly.
Dave Gerr is a naval architect based in New York City and director of the Westlawn Institute of Marine Technology.

